PERCOBAAN 9
TRANSFORMASI LAPLACE, TRANSFORMASI FOURIER
DAN TRANSFORMASI Z
DAN TRANSFORMASI Z
Tujuan
Praktikum
- Mahasiswa dapat mentransformasikan dari fungsi waktu menjadi fungsi Laplace, Fourier, dan Z.
- Mahasiswa dapat membuat program dalam bahasa MATLAB untuk mentransformasikan dari fungsi waktu menjadi fungsi Laplace, Fourier, dan Z ___________________________________________________
9.1 Dasar
Teori
9.1.1 Transformasi Laplace
Transformasi Laplace merupakan suatu model
matematis yang dapat dipergunakan untuk mempemudah dalam penghitungan
matematis. Definisi Tranformasi Laplace
Tabel 1. Sifat
Transformasi Laplace
Teorema
|
Domain Waktu
|
Domain Frekuensi Komplek
|
|
1
|
Linieritas
|
c1f1(t)+c2f2(t)+…
…+cnfn(t)
|
c1F1(s) + c2F2(s)
+......
...... + cnFn(s)
|
2
|
Pergeseran
Waktu
|
f(t-a)uo(t-a)
|
e-asF(s)
|
3
|
Pergeseran
Frekuensi
|
e-asf(t)
|
F(s+a)
|
4
|
Penskalaan
Waktu
|
f(at)
|
|
5
|
Diferensiasi
Waktu
|
sF(s)-f(0-)
|
|
6
|
Diferensiasi
Frekuensi
|
||
7
|
Integrasi
Waktu
|
||
8
|
Integrasi
Frekuensi
|
||
9
|
Periodasitas
Waktu
|
F(t+nT)
|
|
10
|
Teorema
Nilai Inisial
|
||
11
|
Teorema
Nilai Akhir
|
||
12
|
Konvolusi
Wktu
|
f1(t)*f2(t)
|
F1(s)F2(s)
|
13
|
Konvolusi
Frekuensi
|
f1(t)f2(t)
|
Tabel
2. Transformasi Laplace untuk beberapa fungsi yang umum digunakan:
f(t)
|
F(s)
|
|
1
|
u0(t)
|
1/s
|
2
|
tu0(t)
|
1/s2
|
3
|
tnu0(t)
|
n!/sn+1
|
4
|
1
|
|
5
|
e-as
|
|
6
|
e-atu(t)
|
|
7
|
tne-atu0(t)
|
|
8
|
||
9
|
||
10
|
e-at
|
|
11
|
e-at
|
Penggunaan Laplace
Misal, dalam suatu analisis sistem dengan
transformasi Laplace, didapat sinyal keluaran memiliki memiliki bentuk dalam
domain kompleks sebagai berikut.
Untuk mendapatkan nilai di domain waktu,
digunakan fraksionalisasi atau teorema residu kemudian transformasi balik.
Biasanya, setelah dipecah menjadi sejumlah suku pecahan, transformasi balik
menjadi mudah karena bentuknya adalah bentuk umum.
Catatan:
Pole adalah nilai yang membuat nilai
fungsi menjadi tak berhingga
Zero adalah nilai yang
membuat nilai fungsi menjadi nol
9.1.2 Transformasi Fourier
Definisi
Tabel 3. Sifat transformasi
Fourier:
f(t)
|
F(ω)
|
|
Linieritas
|
a1f1(t)+a2f2(t)+....
|
a1F1(ω)+
a2F2(ω)+....
|
Simetri
|
f(t)
|
2πf(-ω)
|
Penskalaan Waktu
|
fa(t)
|
|
Pergeseran Waktu
|
fa(t-t0)
|
F(ω)e-j
ωto
|
Pergeseran Frekuensi
|
e-j ωtof(t)
|
F(ω- ω0)
|
Diferensiasi Waktu
|
||
Diferensiasi Frekuensi
|
(-jt)nf(t)
|
|
Integrasi Waktu
|
||
Fungsi Konjugate
|
f*(t)
|
F*(-ω)
|
Konvolusi Waktu
|
f1(t)+f2(t)
|
F1
(ω).F2(ω)
|
Konvolusi Frekuensi
|
f1(t).f2(t)
|
|
Area under
|
||
Area under F(w)
|
F(0)=
|
|
Teorema Parseval
|
||
Tebl
4. Fungsi dalam bentuk transformasi Fourier yang sering digunakan
f(t)
|
F(ω)
|
δ (t)
|
1
|
δ (t-t0)
|
e-jωto
|
1
|
2πδ(ω)
|
e-jωto
|
2πδ(ω- ωo)
|
sgn(t)
|
2/(j(ω)
|
uo(t)
|
|
cos ωot
|
fπ[δ(ω- ωo)+( ω+ ωo)]
|
sin ωot
|
fπ[δ(ω- ωo)-( ω+ ωo)]
|
e-atuo(t)
a>0
|
a>0
|
te-atuo(t)
a>0
|
a>0
|
e-atcos ωotuo(t)
a>0
|
; a>0
|
e-atsin ωotuo(t)
a>0
|
|
A[uo(t+T)-uo(t-T)]
|
2AT
|
7.1.3 Transformasi Z
Definisi:
Tabel 5. Sifat
transformasi z
Teorema
|
Domain
Waktu
|
Transformasi
Z
|
Linieritas
|
af1[n]+bf2[n]+....
|
aF1(z)+bF2(z)+....
|
Pergeseran
dari x[n]uo[n]
|
f[n-m]u0[n-m]
|
z-mF(z)
|
Geser
Kanan
|
f[n-m]
|
z-mF(z)+
|
Geser
kiri
|
f[n+m}
|
zmF(z)+
|
Perkalian
dengan an
|
anf[n]
|
|
Perkalian
dengan e-naT
|
e-naTf[n]
|
F(eaTz)
|
Perkalian
dengan n
|
nf[n]
|
|
Perkalian
dengan n2
|
n2f[n]
|
|
Penjumlahan
dalam waktu
|
||
Konvolusi
waktu
|
f1[n]*f2[n]
|
F1(z)*F2(z)
|
Teorema
Nilai Inisial
|
||
Teorema
Nilai Akhir
|
||
Tabel 6. Transformasi Z dari fungsi yang sering
digunakan
f(t)
|
F(ω)
|
δ (n)
|
1
|
δ ( n-m)
|
z-m
|
anu0[n]
|
|
u0[n]
|
|
(e-naT)u0[n]
|
|
(cos naT)uo[n]
|
|
(sin aT)uo[n]
|
|
(ancos naT)uo[n]
|
|
(ansin naT)uo[n]
|
|
uo[n]=uo[n-m]
|
|
nuo[n]
|
z/(z-1)2
|
n2uo[n]
|
Z(z+1)/(z-1)3
|
[n+1]uo[n]
|
Z2/(z-1)2
|
annuo[n]
|
(az)/(z-a)2
|
ann2uo[n]
|
Az(z+a)/(z-a)3
|
ann[n-1]uo[n]
|
2az2/(z-a)3
|
9.2.
Peralatan
- PC multimedia yang sudah dilengkapi dengan OS Windows
- Perangkat Lunak Matlab yang dilengkapi dengan
Tool Box DSP
9.3. Langkah
Percobaan
9.3.1 Langkah Percobaan Transformasi Laplace
Sebagai contoh, kita akan menentukan fungsi
Laplace berikut ini dalam domain waktu:
Dari Tabel, didapat bahwa
Maka:
Dengan Matlab, fungsi yang bisa
digunakan adalah factor(polynom), residue(num,den),
ilapace(Fs).
Factor
>> syms s
>>
factor(s^3 + 12*s^2 + 44*s + 48)
ans =
(s+4)*(s+2)*(s+6)
Fungsi factor memiliki kekurangan ketika harus memfaktorkan suatu polinom
bila ada akar yang berupa bilangan kompleks. Sebagai gantinya, gunakan fungsi
roots(polynom).
Residue
>> Ns=[3
2];
>> Ds=[1
3 2];
>> [r p
k]residue(Ns,Ds)
r =
4
-1
p =
-2
-1
k =
[]
Ilaplace
>>
syms s
>>
Fs=(3*s+2)/(s^2+3*s+2);
>>
ft=ilaplce(Fs)
ft = 4*exp(-2*t)-exp(-t)
7.3.3
Langkah Percobaan Fourier
Transformasi Fourier dengan
Matlab
>>
syms t v w x;
>>
ft=exp(0.5*(-t^2));
>>
Fw=fourier(ft)
Fw =
2^(1/2)*pi^(1/2)*exp(-1/2*w^2)
>>
pretty(Fw)
1/2
1/2 2
2 pi
exp(- 1/2 w )
>>
ft=ifourier(Fw)
ft =
exp(-1/2*x^2)
7.3.3
Langkah Percobaan Transformasi Z
Berikut ini ditunjukkan contoh transformasi Z, termasuk penurunannya. Silakan
diamati / dimengerti langkah-langkah penurunannya, lanjutkan dengan ujicoba
pembuatan program MATLAB-nya.
Gunakan metoda fraksionalisasi untuk inverse z transform
dari fungsi berikut:
Penyelesaian
Dari tabel bentuk umum, didapat
Sehingga
f[n]=2(0,5)n-9(0,75)n+8
Berikut ini adalah pemeriksaan
dengan Matlab
>> syms n z;
>> fn=2*(0.5)^n-9*(0.75)^n+8;
>> Fz=ztrans(fn)
Fz =
4*z/(2*z-1)-12*z/(4/3*z-1)+8*z/(z-1)
>> simple(Fz)
ans =
8*z^3/(2*z-1)/(4*z-3)/(z-1)
>> iztrans(Fz)
ans =
2*(1/2)^n-9*(3/4)^n+8
9.4
Analisis Data
Seperti biasa diakhir
pertemuan anda harus menyelesaikan laporan, dengan memberikan bukti-bukti bahwa
anda telah melakkan pecobaan dan jangan lupa menjawab pertanyan atau perintah
yang telah disediakan pada percobaan di atas.
9.5
Tugas
1.
Tentukan transformasi
Fourier untuk fungsi impul satuan [d(t-to)]
2.
Tentukan transformasi Fourier dari sebuah fungsi
singularitas yang dikenal sebagai fung si signum, sgn (t), yang disefinisikan
oleh :
sgn (t)
= u(t) – u(-t)
3.
Tentukan transformasi Fourier untuk fungsi tangga satuan [u(t)].
4. Tentukan
transformasi Fourier
untuk fungsi eksponensial e-at u(t).
5.
Misalkan vi(t) = 10 e-2t u(t) V dalam jaringan
linier dengan h(t) = 2,5 e-8t u(t). carilah : H(jw), Vi(jw); Vo(jw), dan kemudian : (a) vo(0,5)
; (b) vo(1,5); (c) vo,maks
6.
Pada sebuah sistem linier diketahui mempunyai fungsi
sistem [H(jw)]
= .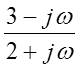 Tentukanlah respons dari sistem linier tersebut, bila
masukannya adalah : (a) d(t); (b) u(t) ;
(c) sgn(t)
Tentukanlah respons dari sistem linier tersebut, bila
masukannya adalah : (a) d(t); (b) u(t) ;
(c) sgn(t)
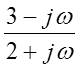 Tentukanlah respons dari sistem linier tersebut, bila
masukannya adalah : (a) d(t); (b) u(t) ;
(c) sgn(t)
Tentukanlah respons dari sistem linier tersebut, bila
masukannya adalah : (a) d(t); (b) u(t) ;
(c) sgn(t)










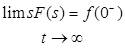




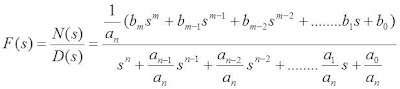











Tidak ada komentar:
Posting Komentar