PERCOBAAN 12
FUZZY DAN
ANFIS
Tujuan Praktikum
-
Memahami konsep dasar FUZZY dan ANFIS dalam kaitannya dengan pengolahan
sinyal
-
Mempu mendesain dan membuat program untuk fuzzy dan
Anfis dan aplikasinya
12.1 Teori Dasar
13.1.1 Fuzzy
Logika fuzzy merupakan sebuah logika yang
memiliki nilai kekaburan atau kesamaran (fuzzyness)
antara benar an salah. Dalam logika fuzzy
sebuah nilai bisa bernilai benar dan salah secara bersamaan namum berapa besar
kebenaran dan kesalahan suatu nilai tergantung kepada bobot keanggotaan yang
dimiliki.
Dalam teori logika fuzzy dikenal himpunan fuzzy
yang merupakan pengelompokan sesuatu berdasarkan variabel bahasa, yang
dinyatakan dalam fungsi keanggotaan. Di dalam semesta pembicaraan U, fungsi keanggotaan dari suatu
himpunan fuzzy tersebut bernilai
antara 0,0 sampai dengan 1,0. Sebagai contoh, himpunan dari temperatur dapat dinyatakan dengan: dingin,
sejuk, normal, hangat, panas. Grafik dari himpunan suhu ini ditunjukkan pada
gambar 12.1.
Gambar 13.1. Contoh Keanggotaan Himpunan
Temperatur
Himpunan dari kecepatan dapat dinyatakan dengan:
lambat, cepat, sangat cepat. Grafik dari himpunan kecepatan ini ditunjukkan
pada gambar berikut:
Gambar 13.2
Contoh Keanggotaan Himpunan Kecepatan
Fungsi dari keanggotaan suatu himpunan fuzzy dinyatakan dengan derajat
keanggotaan suatu nilai terhadap nilai, tegasnya yang berkisar antara 0,0
sampai dengan 1,0. Fungsi keanggotaan suatu himpunan fuzzy dapat dinyatakan dengan fungsi segitiga, trapesium, atau
Gauss.
Cara kerja logika fuzzy. Dalam sistem kontrol logika fuzzy terdapat beberapa tahapan operasional yang meliputi: fuzzifikasi,
penalaran, aturan dasar, dan defzzifikasi.
Gambar 13.3 Blok Diagram Kontol Fuzzy
Fuzzyfikasi.
Fuzzyfikasi adalah suatu prosses peubhan nlai nyata yang ada ke dalam fungsi
keanggotaan.Misalnya pada Gambar 13.4, fuzyfikasi dari suhu 35oC
adalah:
µA1 = 2/3 dan µA2 = 1/3 .
Gambar 13.4 Fungsi Fuzzyfikasi Suatu Sinyal
Aturan Dasar (rule based). Aturan dasar pada kontrol logika fuzzy merupakan bentuk aturan
relasi/implikasi ”Jika-Maka” atau ”If –
Then” seperti pada pernyataan berkut:
” Jika” X = A dan ”Jika” Y=B ”Maka” Z=C
Contoh
dari aturan ini, misalnya diimplementasikan pada pengaturan suhu rungan
menggunakan kipas angin, dapat dinyatakan seperti berikut:
1. ” Jika” suhu panas dan
2. ”Jika” kecepatan
kipas sngat lamba
3. ”Maka” frekuensi sumber dinaikkan sangat tinggi agar kecepatan kipas tinggi
Jadi aturan
dasar ditentukan sesuai dengan
karakteristik objek yang akan dikendlikan. Aturan dasar tersebut dapat
dinyatakan dalam bentuk matrik aturan dasar. Contoh aturan dasar dari rancangan
pengaturan suhu ruangan dapat dilihat pada tabel 7.
Tabel 7.
Contoh Matrik Aturan Dasar Perancangan Kontrol Logika Fuzzy
Y
X
|
B
|
S
|
K
|
|
B
|
K
|
K
|
B
|
Z
|
S
|
K
|
S
|
K
|
|
K
|
B
|
K
|
B
|
|
Dimana:
X: Suhu, Y:
Kecepatan Kipas dn Z: Sumber Frekuensi
B: Besar, S:
Sedang, K: Kecil
|
||||
Penalaaran Kontrol Logika
Fuzzy. Dalam menalar
nilai masukan guna penentuan nilai keluaran sebagai bentuk pengambil keputusan.
Salah satu model penalaran yang banyak dipakai adalah penalaran max-min. Dalam
penalaran model max-min proses pertama
yang dilakukan adalah melakukan min
sinyal keluaran lapisan fuzzifikasi, yang diteruskan dengan opeasi max untuk mencari nilai keluaran yang
selanjutnya akan difuzzyfikasikan sebagai bentuk keluaran pengontrol.
Operasional max-min tersebut dapat
dinyatakan sebagai berikut:
Operasi
Min/Irisan
a ∩ b = min(a,b) = a if a ≤ b dan
b if a > b
Operasi Min/Irisan
a U b =
min(a,b) = a if a ≥ b dan b if a < b
Proses operasi penalaran max-min dapat dijelaskan dengan grafik berikut ini:
Deffuzifikasi. Merupakan proses pemetaan fuzzy kehimpunan tegas (crips). Proses ini merupakan kebalikan
dari proses fuzzyfikasi. Proses defuzzifikasi dinyatakan sebagai berikut:
Z* = defuzzier Z
Dimana:
Z =
Hasil penalaran fuzzy
Z* =
Keluaran kontrol FL
Metode
dalam melakukan defuzzifikasi antara lain:
1. Metoda Max (Maximum)
Metoda ini juga dikenal dengan metoda
puncak dimana nilai keluaran dibatasi oleh fungsi: µc(z*) > µc 1 (z)
2. Metoda Titik Tengah (Center of Area)
Metoda ini juga disebut puat area. Ini lazim
dipakai dalam proses defuzzikasi. Metoda ini diekspresikan dengan persamaan
berikut:
3. Metoda Rata-rata (Average)
Metoda ini digunakan untuk fungsi
keanggotaan keluaran yang simetris. Peersamaan dari metoda ini adalah:
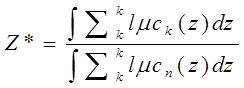
5. Metoda Titik Tengah Area
Terbesar
Dalam Metoda ini dipilih
beradasarkan titik pusat area terbesar yang ada. Metoda ini dinyatakan dalam
bentuk:
Selanjutnya keluaran dari defuzzifikasi tersebut akan digunakan sebagai KLF
13.1.2 Sistem Adaptif Neuro Fuzzy
Adaptive Neuro-Fuzzy
Inference System (ANFIS)
adalah penggabungan mekanisme sistem inferensi fuzzy yang digambarkan dalam arsitektur jaringan syaraf. Sistem adaptif neuro fuzzy berbasis inferensi fuzzy mempunyai dua parameter; yaitu
parameter premis dan konsekuensi. Dalam pelatihan ini dilakukan dua arah yaitu
langkah maju dan langkah balik. Berikut ini ditunjukkan contoh mekanisme
inferensi fuzzy Tagaki-Sugeno-Kang
(TSK) orde satu dengan dua masukan x dan
y (Gambar 13.6). Basis aturan dengan dua aturan fuzzy if-then sebagai berikut:
Rule 1 : if
x is A1 and y is B1 then f1 = p1x + q1y + r1
premis
consequent
Rule 2 : if
x is A2 and y is B2 then f2 = p2x + q2y + r2
premis consequent
Input :
x dan y. Consequent-nya adalah f
Pada suatu masukan crisp (tidak fuzzy) x dan
y. x adalah harga variabel yang dikontrol yaitu pada saat ke t, dan y
pengukuran pada saat ke t+1 sedangkan
f adalah nilai tegangan yang
diberikan sebagai sinyal kontrol. Harga x
dan y tersebut jelas bukan fuzzy. Lalu nilai x dan y tersebut
dipetakan pada funggsi keanggotaannya.
Tiap input dibagi jadi 2 fungsi keanggotaan, x
dibagi dalam A1 dan A2. A1 menyatakan small
dan A2 menyatakan big. Begitu juga y
dibagi dalam fungsi keanggotaan B1 yang menyatakan small dan B2 yang menyatakan big.
Dari pemetaan tersebut x dan y sudah jadi variabel
fuzzy yang masing-masing punya nilai small dan big tertentu. Variabel x mempunyai nilai mA1 dan mA2 sedangkan y
punya nilai mB1 dan mB2. Nilai masing-masing pasangan masukan tersebut
diagregasi dengan operasi T-norm, misalnya operasi AND. Jadi w1 = (mA1 AND mA2)
sedangkan w2 = (mB1 AND mB2). Dari basis aturan yang sudah dibuat, diketahui:
if w
= w1 then
f1 = p1x + q1y + r1
if
w = w2 then
f2 = p2x + q2y + r2
Jadi hasil akhirnya adalah f1 dan f2, yang merupakan
nilai keluaran sinyal control.
Paramter p1, q1,
r1, p2, q2, dan r2 namanya
parameter konsekuen yang ditentukan dengan nilai awal tertentu dan akan berubah
dengan pembelajaran (algoritma belajar). Selanjutnya dari nilai f1 dan f2 ini
kita perlu mendapatkan satu nilai tegangan sebagai sinyal kontrol. Nah nilai
akhir tersebut dihitung dengan persamaan:
Ini yang disebut sebagai
defuzzyfikasi. Rumus tersebut
diperoleh dari metode rata-rata tengah (centroid).
Arsitektur ANFIS
Struktur ANFIS yang menggambarkan sistem fuzzy TSK ditunjukan pada Gambar 13.7,
yang dikenal sebagai arsitektur jaringan syaraf feedforward seperti ini. Diagram blok terdiri dari lima lapis, dan
pada setiap lapis terdapat node.
Terdapat dua macam node yaitu node adaptif dan node tetap.
Fungsi dari
setiap lapis adalah sebagai berikut (Widodo, Thomas Sri; 2005):
Lapis
1 :
Setiap node i pada lapis 1 ini adalah node
adaptif dengan fungsi node sebagai
berikut:
O1i = mAi(x) untuk
i = 1, 2 dan
O1i = mBi-2(y) untuk
i = 3, 4
Dengan x dan y adalah
masukan pada simpul i, Ai (atau Bi-2) adalah fungsi keanggotaan masing-masing
simpul yang merupakan label linguistik yang terkait dengan node tersebut. Simpul O1,i berfungsi untuk
menyatakan derajat keanggotaan tiap masukan terhadap himpunan fuzzy A1,
A2, atau B1, B2. Fungsi keanggotaan yang dipakai adalah jenis
generalized bell (gbell). Parameter
a, b, c, pada fungsi keanggotaan gbell dinamakan parameter premis yang adaptif.
Fungsi keanggotaan fuzzy input
(premis) yang digunakan adalah fungsi Generalized-Bell:
Fungsi Generalized-Bell akan dipakai sebagai
fungsi keanggotaan dari masukan, dan ditentukan sekehendak sebagai parameter
awal a, b, c dan jumlah himpunan fuzzy input. Nantinya parameter premis a,b,c
akan diubah dengan cara pembelajaran.
Lapis 2
Semua simpul pada lapisan ini adalah nonadaptif
(parameter tetap). Fungsi simpul ini adalah mengalikan setiap sinyal masukan
yang datang. Fungsi simpul:
O2i = wi = mAi(x).m Bi(y), i = 1,2
Setiap node dari lapis ini menyatakan kuat
penyulutan dari aturan.
Lapis 3
Tiap keluaran simpul menyatakan derajat
pengaktifan tiap aturan fuzzy. Fungsi
ini dapat diperluas apabila bagian premis memiliki lebih dari dua himpunan fuzzy. Banyaknya simpul pada lapisan ini
menunjukkan banyaknya aturan yang dibentuk. Fungsi perkalian yang digunakan
adalah kata hubung and dengan menggunakan operator t-norm.
Setiap simpul pada lapisan ini adalah
nonadaptif yang menampilkan fungsi derajat pengaktifan ternomalisasi (normalized firing strength) yaitu rasio
keluaran simpul ke-i pada lapisan sebelumnya terhadap seluruh keluaran lapisan
sebelumnya, dengan bentuk fungsi simpul:
Apabila dibentuk lebih
dari dua aturan, fungsi dapat diperluas dengan membagi wi dengan
jumlah total w untuk semua aturan. Keluaran lapis ini disebut kuat penyulutan
ternormalisasi
Lapis 4
Setiap node pada lapis ini adalah node adaptif
dengan fungsi node:
O4,i = wi fi = wi(pix
+ qiy + ri )
Dengan
Wi :
kuat penyulutan ternormalisasi dari lapis 3
(pi, qi, ri
) : himpunan parameter dari node.
Parameter pada lapis ini dise-but sebagai parameter konsekuensi yang adaptif.
Lapis 5
Node
tunggal pada lapis ini adalah node
tetap berlabel £ yang menghitung keluaran keseluruhan sebagai penjumlahan semua
sinyal yang datang. Fungsi
simpul:
Jaringan adaptif dengan lima lapisan tersebut
ekivalen dengan sistem inferensi fuzzy TSK.
Algoritma Pelatihan Hibrid
Pada struktur ANFIS Gambar 13.8, simpul adaptif
terdapat pada lapisan pertama dan keempat. Simpul pada lapisan pertama
mengandung parameter premis yang nonlinier sedangkan pada lapisan keempat
mengandung parameter konsekuen yang linier. Untuk memperbaharui parameter itu,
maka perlu metoda atau algoritma untuk itu. Metoda pembelajaran jaringan syaraf
tiruan banyak macamnya, dan masing2 punya kelebihan dan kekurangan.
13.2 Peralatan
- PC multimedia yang sudah dilengkapi dengan
OS Windows
-
Perangkat Lunak Matlab yang dilengkapi dengan Tool Box DSP
13.3 Langkah Percobaan
13.3.1 Langkah Percobaan Fuzzy
1. Berikut ini akan dibuat pernyataan untuk
pendefinisian. Fungsi keanggotaan dan aturan dasar (rule) yang mendefinisikan
fungsi keluaran. Buatlah program berikut:
subplot(2,1,1),
plotmf(fismat,'input',1)
subplot(2,1,2),gensurf(fismat)
showrule(fismat)
jalankan dan amati apa yang terjadi. Juga
lihat pada command window, apa yang ditampilkan?.
2. Berikutnya, lakukan pembuatan program
seperti berikut dan kemudian jalankan.
a=newfis('tipper');
a=addvar(a,'input','service',[0
10]);
a=addmf(a,'input',1,'poor','gaussmf',[1.5
0]);
a=addmf(a,'input',1,'good','gaussmf',[1.5
5]);
a=addmf(a,'input',1,'excellent','gaussmf',[1.5
10]);
plotmf(a,'input',1)
apa yang
ditampilkan?.
13.3.2
Langkah Percobaan ANFIS
1. Berikutnya, lakukan pembuatan program seperti
berikut dan kemudian jalankan.
x = (0:0.1:10); y =
sin(2*x)./exp(x/5);
trnData = [x y];
numMFs = 5;
mfType = 'gbellmf';
epoch_n = 20;
in_fismat =
genfis1(trnData,numMFs,mfType);
out_fismat
= anfis(trnData,in_fismat,20);
plot(x,y,x,evalfis(x,out_fismat));
legend('Training Data','ANFIS Output');
jelaskan hasil tampilannya?.
Ulangi untuk program berikut:
x = (0:0.1:10)';
z = 0.1*sin(200*x) % noise
y = sin(2*x)./exp(x/5)+z; % sinyal + noise
trnData = [x y];
numMFs = 5;
mfType = 'gbellmf';
epoch_n = 20;
in_fismat =
genfis1(trnData,numMFs,mfType);
out_fismat
= anfis(trnData,in_fismat,20);
plot(x,y,x,evalfis(x,out_fismat));
legend('Training Data','ANFIS
Output');
jelaskan
hasil tampilannya?.
Ulangi
untuk program berikut:
x
= (0:0.1:10);
z
= 0.1*sin(200*x) %
noise
y
= sin(2*x)./exp(x/5)+z; % sinyal + noise
trnData
= [x y];
numMFs
= 5;
mfType
= 'gbellmf';
epoch_n
= 20000;
in_fismat =
genfis1(trnData,numMFs,mfType);
out_fismat
= anfis(trnData,in_fismat,20);
plot(x,y,x,evalfis(x,out_fismat));
legend('Training Data','ANFIS
Output');
jelaskan hasil tampilannya?.
2. Berikutnya, lakukan pembuatan program
seperti berikut dan kemudian jalankan.
x=0:0.1:5;
mfp1 = [1 2 3];
mfp2 =
mf2mf(mfp1,'gbellmf','trimf');
plot(x,gbellmf(x,mfp1),x,trimf(x,mfp2))
jelaskan hasil tampilannya?.
2. Berikutnya, lakukan pembuatan program
seperti berikut dan kemudian jalankan.
for t=118:1117,
Data(t-117,:)=[x(t-18) x(t-12)
x(t-6) x(t) x(t+6)];
end
trnData=Data(1:500,
:);chkData=Data(501:end, :);
fismat
= genfis1(trnData);
subplot(2,2,1)
plotmf(fismat,'
input', 1)
subplot(2,2,2)
plotmf(fismat,'
input', 2)
subplot(2,2,3)
plotmf(fismat,'
input', 3)
subplot(2,2,4)
plotmf(fismat,' input', 4)
jelaskan
hasil tampilannya?.
3. Berikutnya sebuah program yang
harus anda coba, tapi sebelumnya anda harus menyiapkan hal-hal sebagai berikut:
1)
buat sebuah file gambar dan beri nama: 'GambarParameter.jpg' dan
‘Gambar_Tunggu.jpg’, simpan pada work
dari MATLAB.
2) Buat file data dengan nama DataPelatihan1
DataPelatihan2, DataPelatihan3,
DataPelatihan4, DataTarget.
3)
buat program dengan nama Proses_Anfis.m, seperti ditunjukkan pada program di
bawah. simpan pada work dari MATLAB.
4) Lalu buat program seperti berikut ini
dengan nama: Anfis_Parameter.m, dan jalankan.
%--------------------------------------------------------
% Nama File : Anfis_Parameter.m
% Oleh : Yulianto
%--------------------------------------------------------
winAnfisProses=figure(...
'unit','point','position',[230 130 410 310],...
'color',[.8 .8 .9],'menubar','none','resize','on',...
'numbertitle','off','name','Paramter Anfis',...
'WindowStyle','normal');
grafikAnfis21=axes('parent',winAnfisProses,...
'units','point','position',[0 0 410 310],...
'xgrid','on','ygrid','on','xcolor',[.8 .8 .9 ],...
'ycolor',[.8 .8 .9 ],'fontsize',10,...
'color',[.8 .8 .9]),'backgroundColor',[.8 .8 .9];
editInputWav1=uicontrol('parent',winAnfisProses,...
'unit','point','position',[330 5 70 15],...
'backgroundColor',[.5 .8 1],'string','JALANKAN',...
'fontname','fixedsys','fontsize',9,'callback','Proses_Anfis');
editAnfis23=uicontrol('parent',winAnfisProses,...
'unit','point','position',[143 198 60 18],'Style','Text',...
'backgroundColor',[1 1 1],'string','numMFs',...
'fontname','arial black','fontsize',10)
editAnfis24=uicontrol('parent',winAnfisProses,...
'unit','point','position',[205 198 60 17],...
'Style','Edit','backgroundColor',[.2 .9 .2],...
'string','2','fontname','arial black','fontsize',10);
editAnfis25=uicontrol('parent',winAnfisProses,...
'unit','point','position',[143 180 60 18],'Style','Text',...
'backgroundColor',[1 1 1],'string','mfType',...
'fontname','arial black','fontsize',10)
editAnfis26=uicontrol('parent',winAnfisProses,...
'unit','point','position',[205 180 60 17],...
'Style','Edit','backgroundColor',[.2 .9 .2],...
'string','gbellmf','fontname','arial black','fontsize',10);
editAnfis27=uicontrol('parent',winAnfisProses,...
'unit','point','position',[118 163 85 17],'Style','Text',...
'backgroundColor',[1 1 1],'string','num_epochs',...
'fontname','arial black','fontsize',10)
editAnfis28=uicontrol('parent',winAnfisProses,...
'unit','point','position',[205 163 60 17],...
'Style','Edit','backgroundColor',[.2 .9 .2],...
'string','500','fontname','arial black','fontsize',10);
editAnfis29=uicontrol('parent',winAnfisProses,...
'unit','point','position',[139 146 65 18],'Style','Text',...
'backgroundColor',[1 1 1],'string','err_goal',...
'fontname','arial black','fontsize',10)
editAnfis20=uicontrol('parent',winAnfisProses,...
'unit','point','position',[205 146 60 17],...
'Style','Edit','backgroundColor',[.2 .9 .2],...
'string','0.001','fontname','arial black','fontsize',10);
[a,MAP]=IMREAD('GambarParameter.jpg');
image(a); grid off;
Program ke 2 yang harus anda simpan terlebih dahulu
dalam work dari MATLAB.
%-----------------------------------------------------------------------------------------
% Nama File : Proses_Anfis.m
% Oleh : Yulianto
%-----------------------------------------------------------------------------------------
Anfis1=str2num(get(editAnfis24Baru,'String')); num_mf = Anfis1;
Anfis2=get(editAnfis26Baru,'String'); mf_type= Anfis2;
Anfis3=str2num(get(editAnfis28Baru,'String')); num_epochs= Anfis3;
Anfis4=str2num(get(editAnfis20Baru,'String')); err_goal= Anfis4;
pilihanAnfisBaru=(get(editAnfis22Baru,'Value'));
load DataPelatihan1;DataLatih1=DataPelatihan1;
load
DataPelatihan2;DataLatih2=DataPelatihan2;
load
DataPelatihan3;DataLatih3=DataPelatihan3;
load
DataPelatihan4;DataLatih4=DataPelatihan4;
load
DataTarget;DataTarget=DataTarget;
t=length(DataTarget);ii=1:1:t;i=find(ii<=250);
u=DataLatih1(i);v=DataLatih2(i);w=DataLatih3(i);x=DataLatih4(i);
y=DataTarget(i);v=v(i);x=x(i);
pp=DataBaru1(i);
qq=DataBaru2(i);rr=DataBaru3(i); ss=DataBaru4(i);
tt=DataCek(i)
trnData=[ u v w x
y ];chkData=[ pp qq rr ss tt];
% Initialise the system matrix
close('Anfis_Parameter');
winAnfisProses1=figure('unit','point','position',[30
390 650 150],...
'color',[.4 .8 .2],'menubar','none','resize','on',...
'numbertitle','off','name','Data Masukan ANFIS',...
'WindowStyle','normal');axis
off;
subplot(1,4,1);plot(u,'r','linewidth',2);set(gca,'color',[.8
.6 .2]);
subplot(1,4,2);plot(v,'g','linewidth',2);set(gca,'color',[.8
.6 .2]);
subplot(1,4,3);plot(w,'b','linewidth',2);set(gca,'color',[.8
.6 .2]);
subplot(1,4,4);plot(x,'y','linewidth',2);
set(gca,'color',[.8 .6 .2]);
winAnfisProses2=figure('unit','point','position',[30
200 650 150],...
'color',[.8 .8 0],'menubar','none','resize','on',...
'numbertitle','off','name','Fungsi Keanggotaan Awal',...
'WindowStyle','normal');
fismat = genfis1(trnData,num_mf,mf_type);
subplot(1,4,1); plotmf(fismat, 'input',
1);set(gca,'color',[.8 .6 .6]);
subplot(1,4,2); plotmf(fismat, 'input',
2);set(gca,'color',[.8 .6 .6]);
subplot(1,4,3); plotmf(fismat, 'input',
3);set(gca,'color',[.8 .6 .6]);
subplot(1,4,4); plotmf(fismat, 'input',
4);set(gca,'color',[.8 .6 .6]);
close('Fungsi Keanggotaan Awal');
winAnfisProses3=figure('unit','point','position',[30
250 650 150],...
'color',[.8 .8 0],'menubar','none','resize','on',...
'numbertitle','off','name','Fungsi
Keanggotaan Awal1',...
'WindowStyle','normal');
subplot(1,4,1); plotmf(fismat, 'input',
1);set(gca,'color',[.8 .6 .6]);
subplot(1,4,2); plotmf(fismat, 'input',
2);set(gca,'color',[.8 .6 .6]);
subplot(1,4,3); plotmf(fismat, 'input',
3);set(gca,'color',[.8 .6 .6]);
subplot(1,4,4); plotmf(fismat, 'input',
4);set(gca,'color',[.8 .6 .6]);
pause(.3);close('Fungsi Keanggotaan Awal1');
winAnfisProses4=figure('unit','point','position',[30
300 650 150],...
'color',[.8 .8 0],'menubar','none','resize','on',...
'numbertitle','off','name','Fungsi Keanggotaan Awal2',...
'WindowStyle','normal');
subplot(1,4,1); plotmf(fismat, 'input',
1);set(gca,'color',[.8 .6 .6]);
subplot(1,4,2); plotmf(fismat, 'input',
2);set(gca,'color',[.8 .6 .6]);
subplot(1,4,3); plotmf(fismat, 'input',
3);set(gca,'color',[.8 .6 .6]);
subplot(1,4,4); plotmf(fismat, 'input',
4);set(gca,'color',[.8 .6 .6]);
pause(.3);close('Fungsi Keanggotaan Awal2');
winAnfisProses5=figure('unit','point','position',[30
350 650 150],...
'color',[.8 .8 0],'menubar','none','resize','on',...
'numbertitle','off','name','Fungsi Keanggotaan Awal3',...
'WindowStyle','normal');
subplot(1,4,1); plotmf(fismat, 'input',
1);set(gca,'color',[.8 .6 .6]);
subplot(1,4,2); plotmf(fismat, 'input',
2);set(gca,'color',[.8 .6 .6]);
subplot(1,4,3); plotmf(fismat, 'input',
3);set(gca,'color',[.8 .6 .6]);
subplot(1,4,4); plotmf(fismat, 'input',
4);set(gca,'color',[.8 .6 .6]);
pause(.5);
winAnfisProses6=figure('unit','point','position',[30
390 650 150],...
'color',[.8 .8 0],'menubar','none','resize','on',...
'numbertitle','off','name','Fungsi Keanggotaan Awa14',...
'WindowStyle','normal');
subplot(1,4,1); plotmf(fismat, 'input',
1);set(gca,'color',[.8 .6 .6]);
subplot(1,4,2); plotmf(fismat, 'input',
2);set(gca,'color',[.8 .6 .6]);
subplot(1,4,3); plotmf(fismat, 'input',
3);set(gca,'color',[.8 .6 .6]);
subplot(1,4,4); plotmf(fismat, 'input',
4);set(gca,'color',[.8 .6 .6]);
close('Fungsi Keanggotaan Awal3');pause(2);
subplot(1,4,1); plotmf(fismat, 'input',
1);pause(2);set(gca,'color',[1 1 0]);
subplot(1,4,2); plotmf(fismat, 'input',
2);pause(2);set(gca,'color',[1 1 0]);
subplot(1,4,3); plotmf(fismat, 'input',
3);pause(2);set(gca,'color',[1 1 0]);
subplot(1,4,4); plotmf(fismat, 'input', 4);pause(2);set(gca,'color',[1
1 0]);
pause(.3);close('Data Masukan ANFIS');
winAnfisProses8=figure('unit','point','position',[220
200 280 150],...
'color',[.4 .8 .2],'menubar','none','resize','on',...
'numbertitle','off','name','Tunggu: Penentuan Keanggotaan Akhir',...
'WindowStyle','normal');
[a,MAP]=IMREAD('gambarTunggu.jpg'); image(a);
grid off;axis off;
winAnfisProses9=figure('unit','point','position',[30
200 650 150],...
'color',[.4 .8 .2],'menubar','none','resize','on',...
'numbertitle','off','name','Fungsi Keanggotaan Akhir',...
'WindowStyle','normal');
[fismat1,error1,ss,fismat2,error2]=...
anfis(trnData,fismat,[num_epochs],[],chkData);
subplot(1,4,1); plotmf(fismat2, 'input',
1);set(gca,'color',[.9 .6 .2]);
subplot(1,4,2); plotmf(fismat2, 'input',
2);set(gca,'color',[.9 .6 .2]);
subplot(1,4,3); plotmf(fismat2, 'input',
3);set(gca,'color',[.9 .6 .2]);
subplot(1,4,4); plotmf(fismat2, 'input',
4);set(gca,'color',[.9 .6 .2]);
close('Tunggu: Penentuan Keanggotaan
Akhir');pause(3);
subplot(1,4,1); plotmf(fismat2, 'input',
1);pause(2);
set(gca,'color',[0 1 0]);
subplot(1,4,2); plotmf(fismat2, 'input',
2);pause(2);
set(gca,'color',[0 1 0]);
subplot(1,4,3); plotmf(fismat2, 'input',
3);pause(2);
set(gca,'color',[0 1 0]);
subplot(1,4,4); plotmf(fismat2, 'input',
4);pause(2);
set(gca,'color',[0 1 0]);
close('Fungsi Keanggotaan
Akhir');close('Fungsi Keanggotaan Awa14');
winAnfisProses10=figure('unit','point','position',[220
200 280 150],...
'color',[.4 .8 .2],'menubar','none','resize','on',...
'numbertitle','off','name','Tunggu: Penentuan
Keanggotaan Akhir',...
'WindowStyle','normal');
[a,MAP]=IMREAD('GambarTunggu.jpg'); image(a);
grid off;axis off;
winAnfisProses11=figure('unit','point','position',[30
390 650 150],...
'color',[.8 .8 0],'menubar','none','resize','on',...
'numbertitle','off','name','Error',...
'WindowStyle','normal');
plot([error1 error2]);pause(2);
hold on; plot([error1 error2],
'o');set(gca,'color',[1 1 0]);
xlabel('Epochs');ylabel('RMSE (Root Mean
Squared Error)');
title('Error Curves');pause(5);
anfis_output = evalfis([trnData(:,1:4);
chkData(:,1:4)],fismat2,num_epochs);
x=length(anfis_output);xx=1:1:x;
winAnfisProses19=figure('unit','point','position',[30
30 650 150],...
'color',[.4 .8 .2],'menubar','none','resize','on',...
'numbertitle','off','name','Keluaran dan Error',...
'WindowStyle','normal');
y=[y;y];
subplot(211),
plot(xx,anfis_output);
xlabel('Time (sec)'); title('MG Time Series
and ANFIS Prediction');
subplot(212),
plot(xx, y - anfis_output);
close('Tunggu: Penentuan Keanggotaan Akhir');
ErrorAnfisMak=max(y -
anfis_output);ErrorAnfisMin=min(y - anfis_output);
MSE_FFT=mse(y - anfis_output)
winAnfisError=figure('unit','point','position',[220
208 280 150],...
'color',[.4 .8 .2],'menubar','none','resize','on',...
'numbertitle','off','name','Error Maksimum Yang Terjadi',...
'WindowStyle','normal');
editAnfisError1=uicontrol('parent',winAnfisError,...
'unit','point','position',[0 127 110 20],'Style','Text',...
'backgroundColor',[.4 .8 .2],'string','Error Maksimum :',...
'fontname','arial black','fontsize',10)
editAnfisError2=uicontrol('parent',winAnfisError,...
'unit','point','position',[110 127 100 20],'Style','Edit',...
'backgroundColor',[.9 .9 0],'string','Error',...
'fontname','arial
black','fontsize',10)
set(editAnfisError2,'String',num2str(ErrorAnfisMak));
editAnfisError1=uicontrol('parent',winAnfisError,...
'unit','point','position',[0 110 107 20],'Style','Text',...
'backgroundColor',[.4 .8 .2],'string','Error Manimum :',...
'fontname','arial black','fontsize',10)
editAnfisError2=uicontrol('parent',winAnfisError,...
'unit','point','position',[110 107 100 20],'Style','Edit',...
'backgroundColor',[.9 .9 0],'string','Error',...
'fontname','arial black','fontsize',10)
set(editAnfisError2,'String',num2str(ErrorAnfisMin));
editAnfisError1=uicontrol('parent',winAnfisError,...
'unit','point','position',[0 20 107 20],'Style','Text',...
'backgroundColor',[.4 .8 .2],'string','M.S.E. :',...
'fontname','arial
black','fontsize',10)
editAnfisError2=uicontrol('parent',winAnfisError,...
'unit','point','position',[110 20 100 20],'Style','Edit',...
'backgroundColor',[.9 .9 0],'string','Error',...
'fontname','arial black','fontsize',10)
set(editAnfisError2,'String',num2str(MSE_FFT));
editAnfisError3=uicontrol('parent',winAnfisError,...
'unit','point','position',[40 40 170 40],'Style','Text',...
'backgroundColor',[.4 .8 .2],'string','Error',...
'fontname','arial black','fontsize',14)
if MSE_FFT<4.5e-10
Keputusan='WHEEZING ??.. YESS'
else
Keputusan='WHEEZING ??.. NO'
end;
set(editAnfisError3,'String',num2str(Keputusan));
close('Error Maksimum Yang Terjadi');
close('Error');close('Keluaran dan Error');
13.4 Analisis Data
Anda harus menjelaskan
tentang Fuzzy, dan aplikasinya. Jelaskan hasil pemahaman anda dari hasil uji
coba di atas, akan lebih mudah jika anda menggunakan flow chart dalam
menjelaskan program di atas.
13.5 Tugas
1. Beri satu contoh aplikasi fuzzy sederhana.
2. Rancanag sebuah filter untuk membuang
derau dengan menggnakan proggram fuzzy.
3. Buatlah
sebuah program fuzzy yang dapat digunakan untuk mengidentifikasi sinyal suara
dengan menyebutkan sebuah abjad dari 26 abjad.
4. Buatlah
prgram fuzzy yang dapat memanggil sebuah lagu dan sekaligus mengaktifkan lagu
tersebut.
















bermanfaat Sangat percobaannya...
BalasHapusIjin kopas... terima kasih...:)